[最も選択された] 点対称 ��題 275982-6年 点対称 問題
Web右の図は点対称な図形です。 次の問いに答えなさい。 点oを中心にして180度回転させた時、 ①点aと重なる点はどれですか。( ) ②角bと重なる角はどれですか。( ) ③直線ghと重なWeb点対称移動の問題 まずは問題です。 問題 点\(\mathrm{O}\)を回転の中心として、\(\triangle\mathrm{ABC}\)を点対称移動させた\(\triangle{\mathrm{A^\prime B^\primeWeb vol125「点対称なトランプは? 」にチャレンジ! 親子で解ける! 大人も楽しい、算数クイズ! math channelのメンバーたちで考えた「算数クイズ」をWebでも公開!

スマホok 6年 対称な図形 難問に挑戦しよう Youtube
6年 点対称 問題
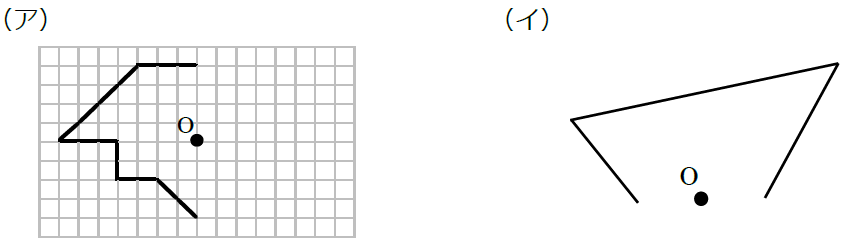
6年 点対称 問題-Web② 点対称な図形とは,1つの点を中心にして180°回転させたとき,もとの図形にきちんと重なる 図形のことです。このときの中心の点を対称の中心といいます。 ポイント 基本問題 対称なWeb下の図形の中から、点対称な図形をすべて選びましょう。 (ア) (イ) (ウ) (エ) (オ) (カ) 下の図について、点アを対称の中心とする、点対称な図形を完成させましょう。
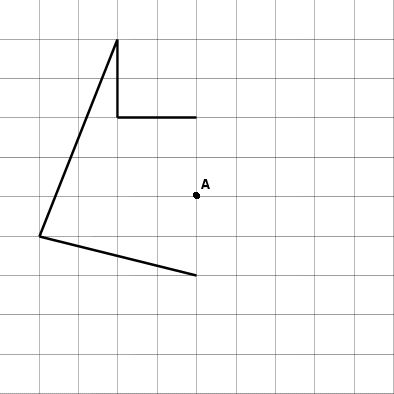



点対称な図形を書く
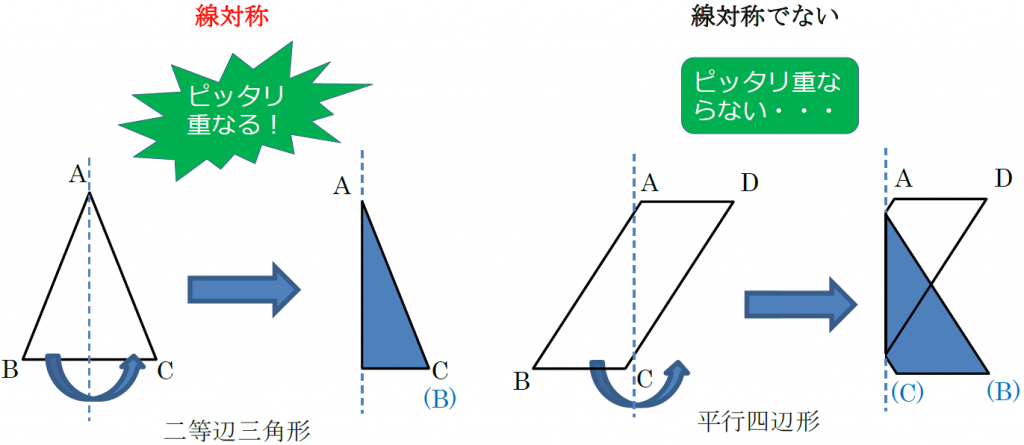
Web今回は高校数学Ⅱで学習する図形と方程式の単元から 「対称な点の座標」 についてイチから解説していきます! 取り上げる問題はこちらです。 問題① 点 に大した次のような点の座Web 次関数 は に関し点対称なグラフになることを示せ. 目次 考え方隅関数・奇関数 偶関数・奇関数について 偶関数とは 奇関数とは 解答 参考3次関数の変曲点についWeb 今回の問題で大切になってくるのは「 線対称 」とか「 点対称 」の意味を正しく理解することです。小学生の受験生にも分かるようにたくさんのイラストを使ってについて
Web 点対称の作図は難しい 子どもたちの作図の様子を見ても、苦戦している子が多いです。 繰り返し練習する機会を与えないといけないなぁと思います。 ↓教科書の合わせたWeb26 minutes ago ブラックオルカの問題点 解決案 以上を踏まえてブッラクオルカの問題点を解決する方法は 入り口を増やす 煙突穴を増やす コットを辞める お座敷スタイルに変更す




線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学




線対称の作図 4つのステップでわかる 対称移動の書き方 Qikeru 学びを楽しくわかりやすく




線対称な図形 無料で使える学習ドリル




点対称な図形を書く
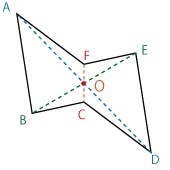



点対称な図形 無料で使える学習ドリル



Q Tbn And9gcsrfn7jp95hepl6xzead Mwmis3gvr I Zbtx2xad99w45evjligln Usqp Cau
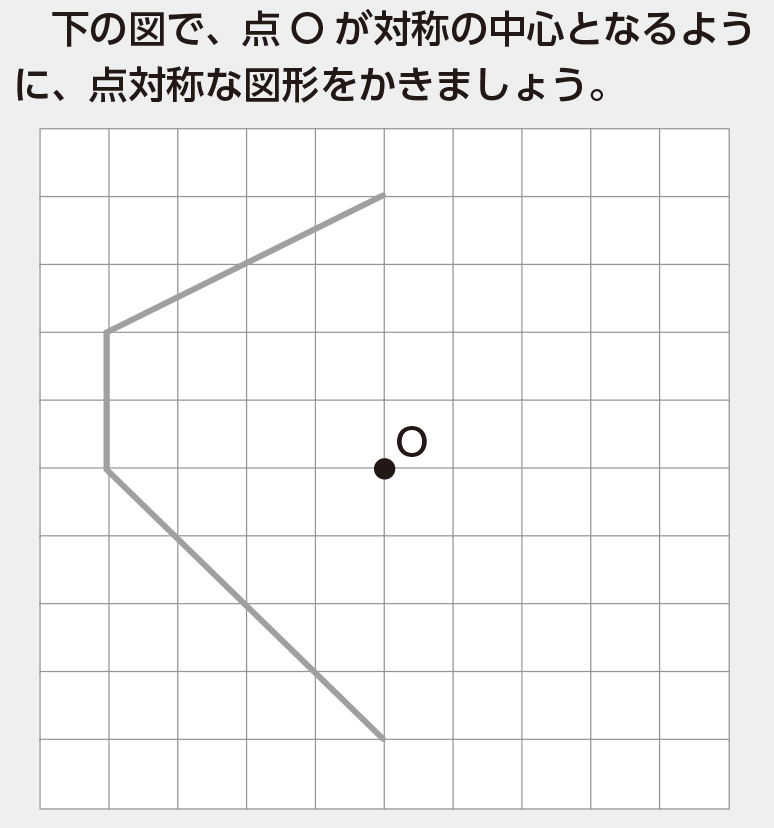



小6算数 対称な図形 点対象 指導アイデア みんなの教育技術
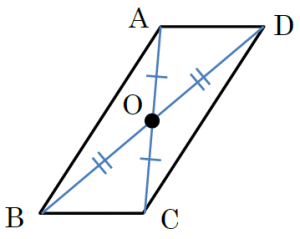



中1数学 点対称な図形とは まなビタミン By 東京個別指導学院
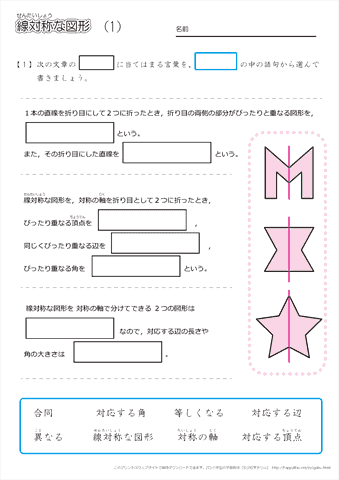



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生
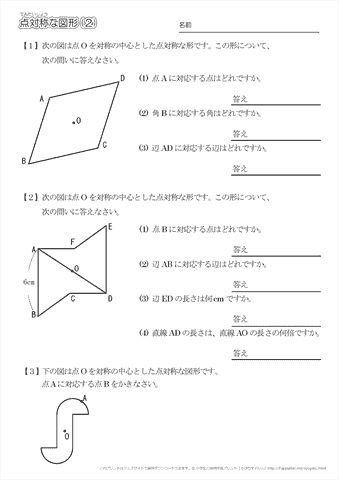



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
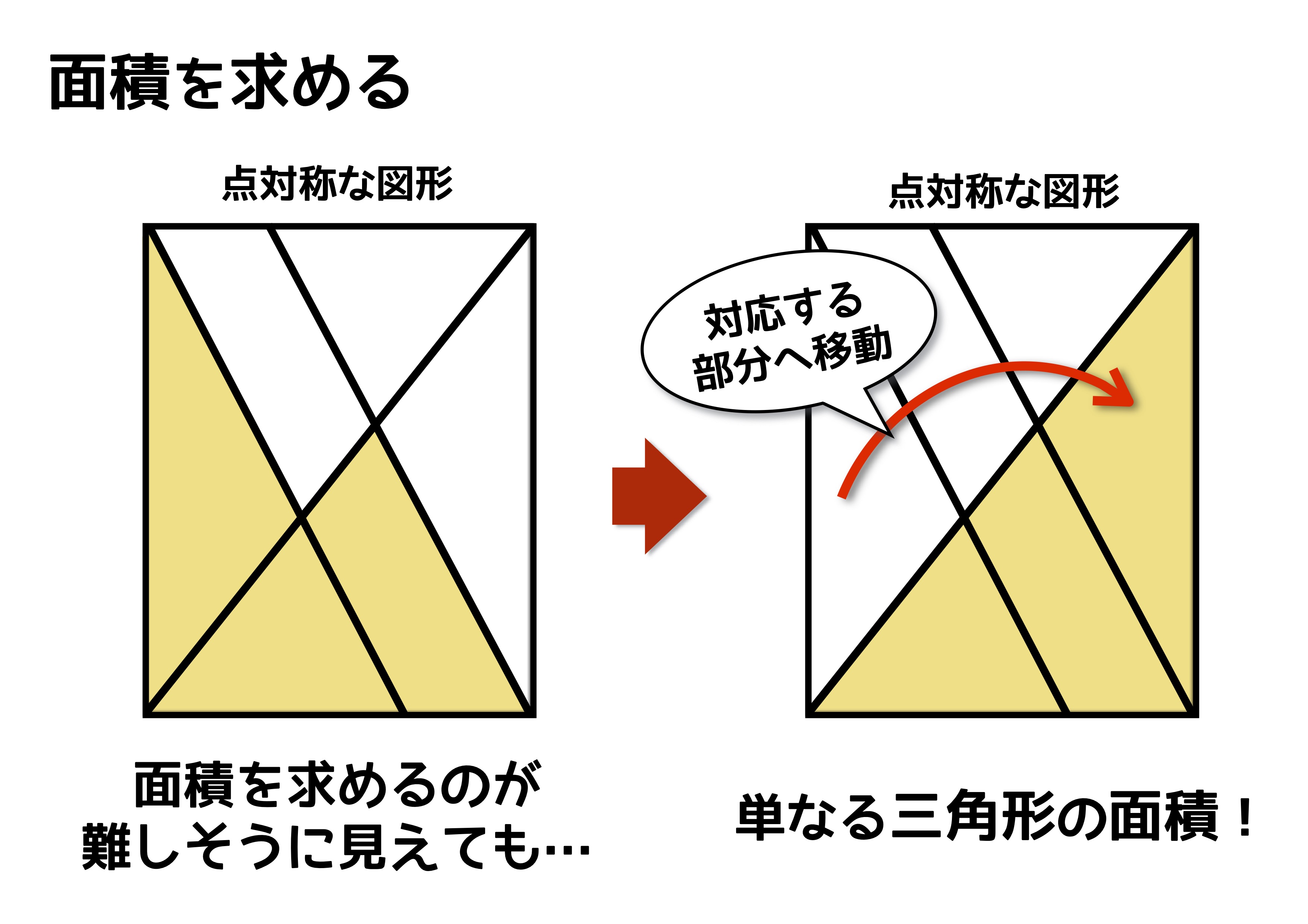



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ



Math 点対称な図形のかき方 働きアリ




算数クイズに挑戦 Vol 125 点対称なトランプは にチャレンジ Mathchannel



中1数学 平面図形3 線対称 点対称 発展問題 問題 136 プリント



線対称図形と点対称図形の見分け方 算数解法の極意
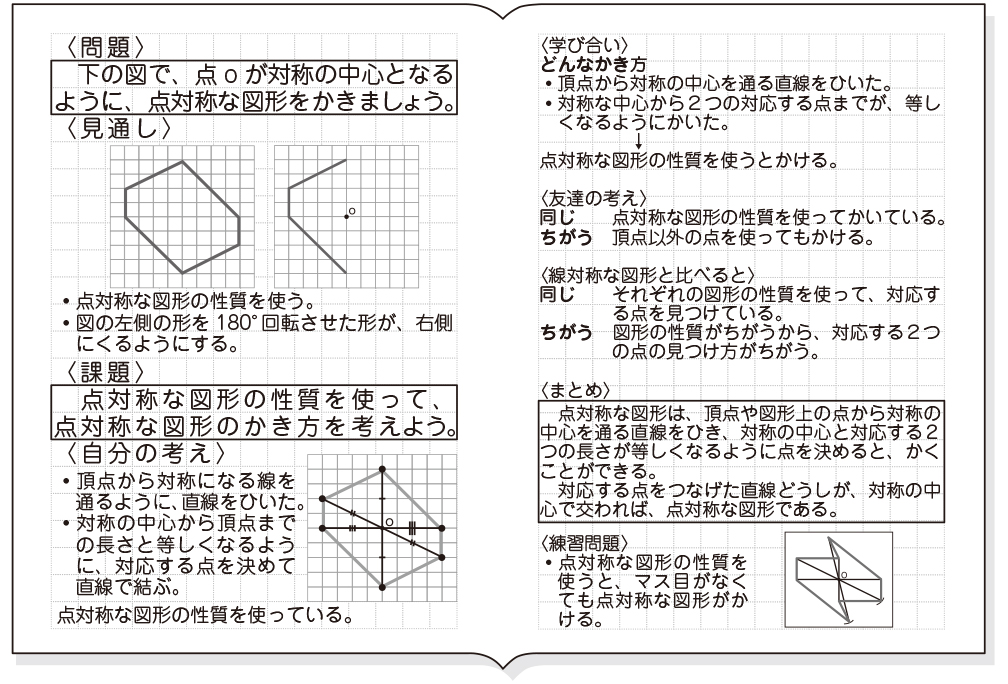



小6算数 対称な図形 点対象 指導アイデア みんなの教育技術
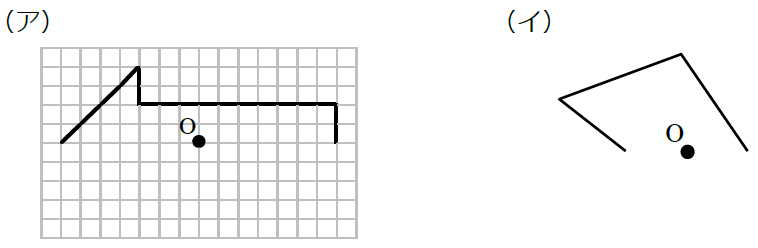



中1数学 点対称な図形とは まなビタミン By 東京個別指導学院



小6算数 対称な図形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ
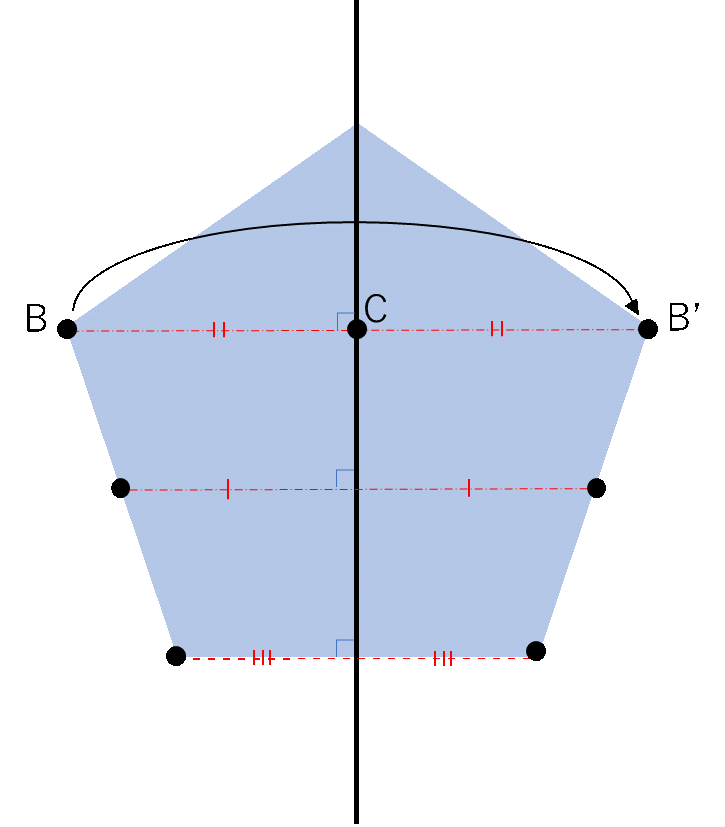



点対称と線対称 算数からやさしく解説 数学 統計教室の和から株式会社
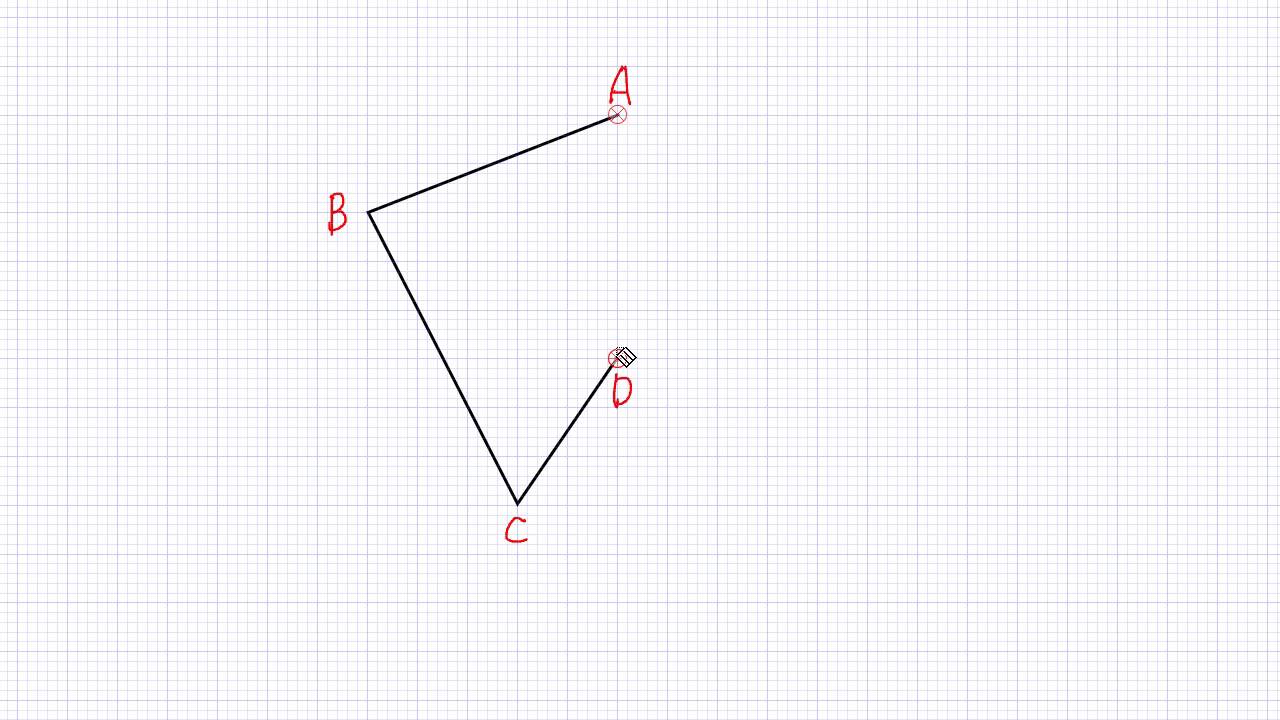



小6 算数 点対称な図形のかき方 Youtube



無料 中1数学 標準問題 解答プリント 135 平面図形2 多角形 点対称




2
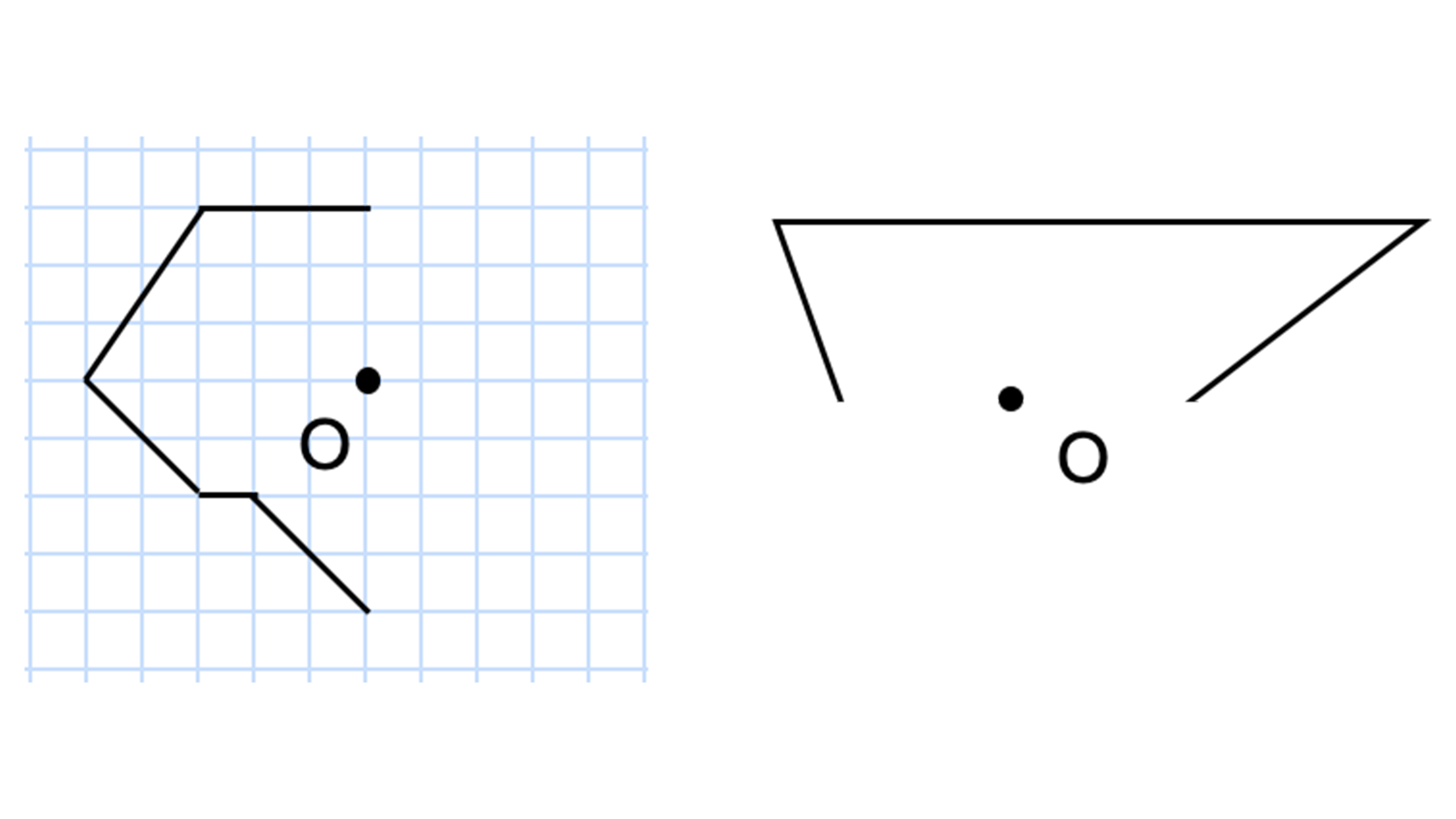



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



Q Tbn And9gcqj6u7ozxekvacu1 5gkoz0xdqtfclfs6zmyr5locfwjis6vax 16ka Usqp Cau
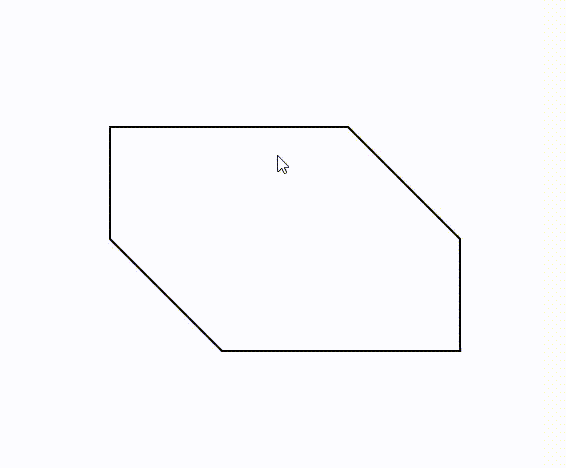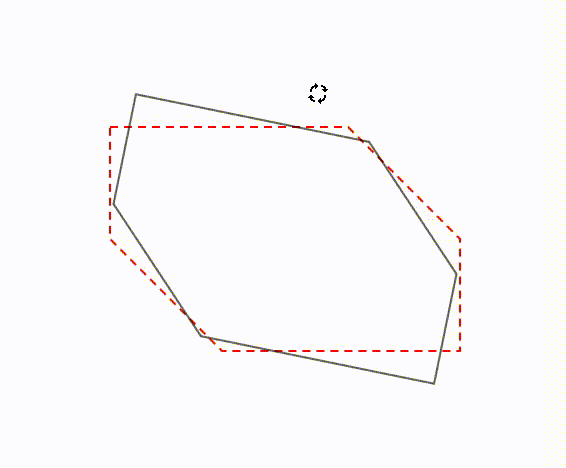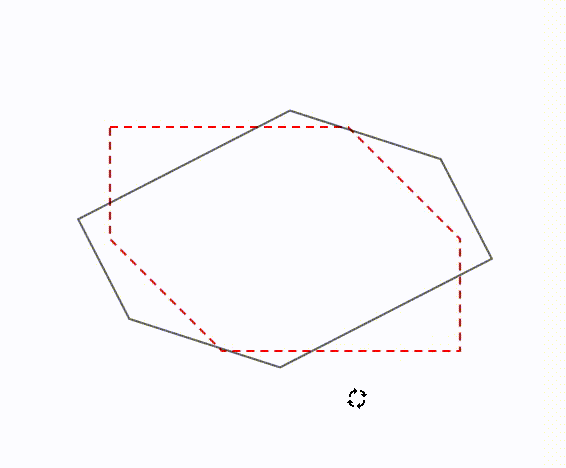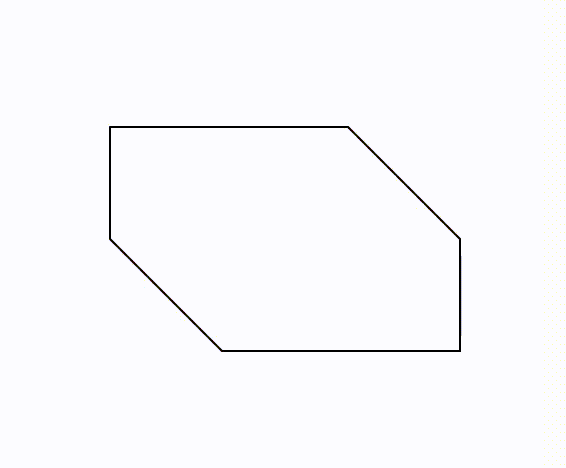



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun
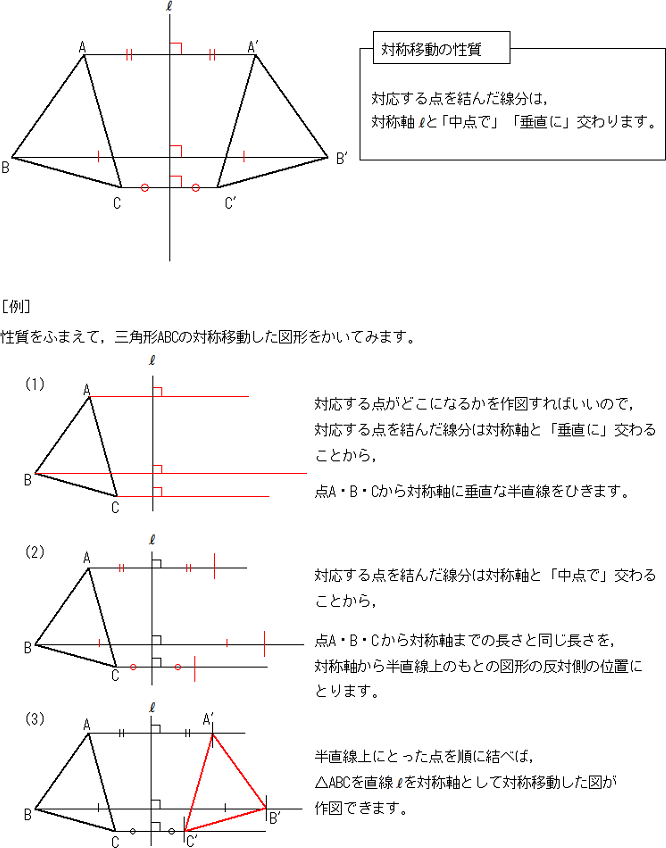



平面図形 対称移動とは何ですか 中学数学 定期テスト対策サイト
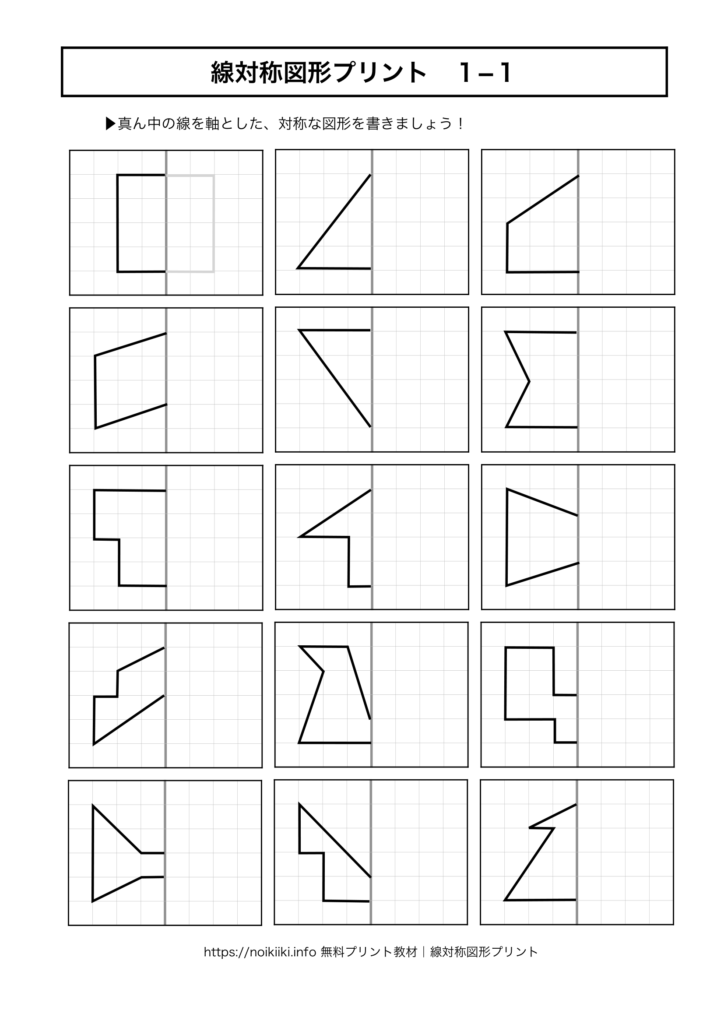



線対称図形プリント1 1 無料で使える脳トレ教材 Noikiiki




対称な図形 Ict教材eboard イーボード
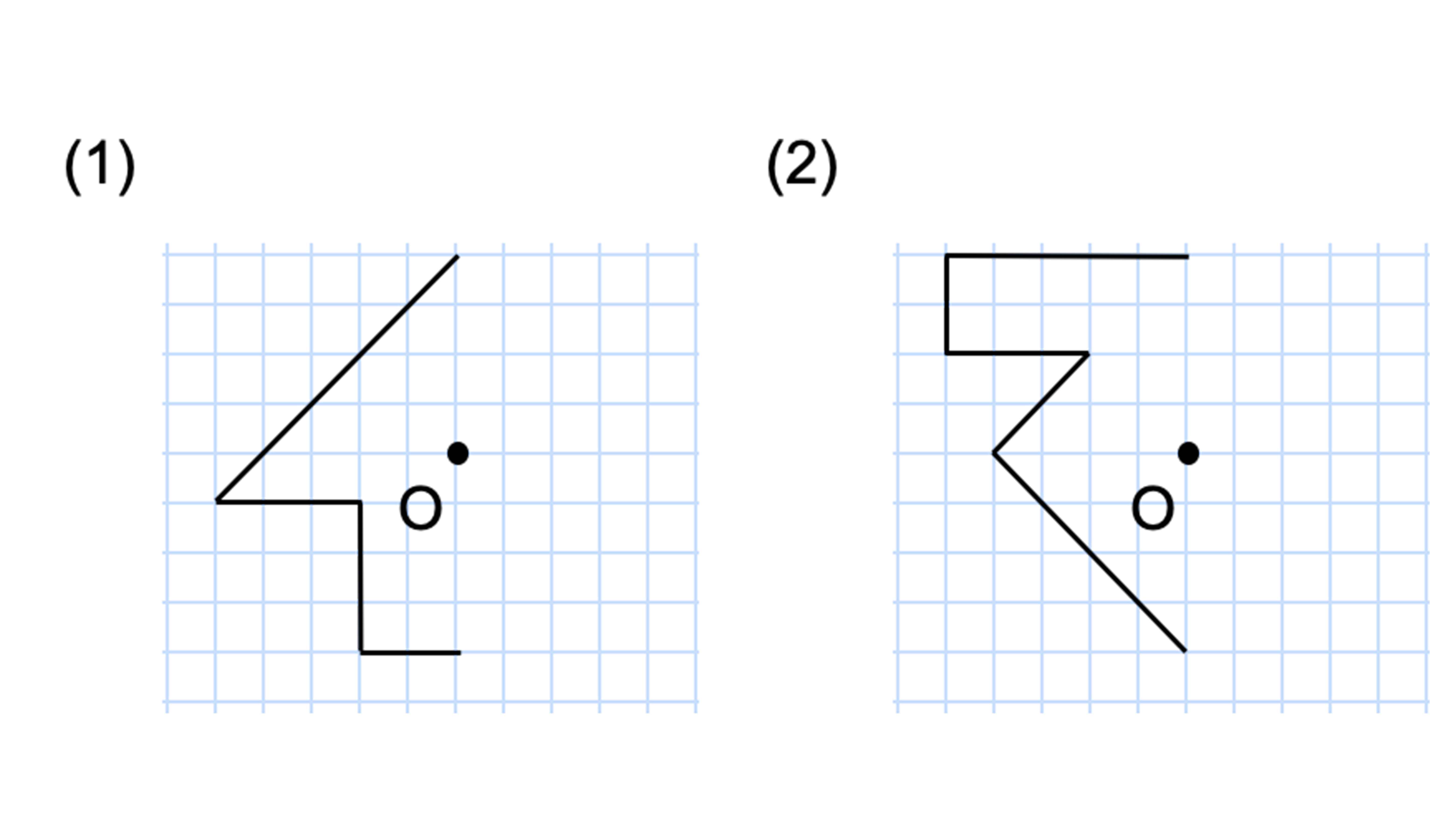



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
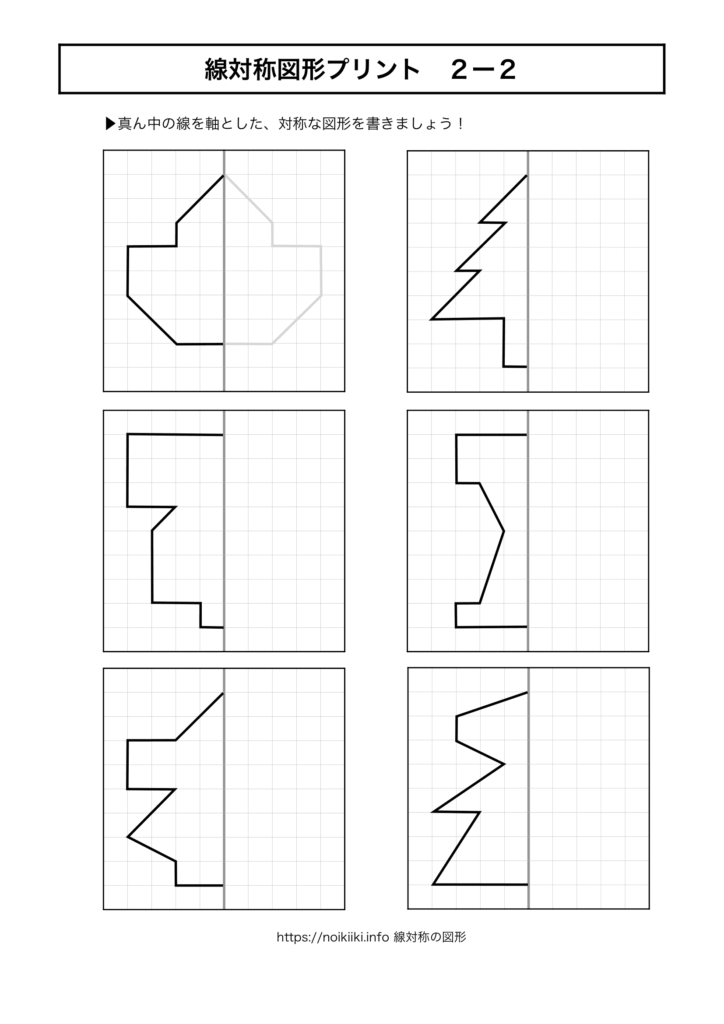



線対称図形プリント2ー2 脳トレ 知育の無料プリント Noikiiki
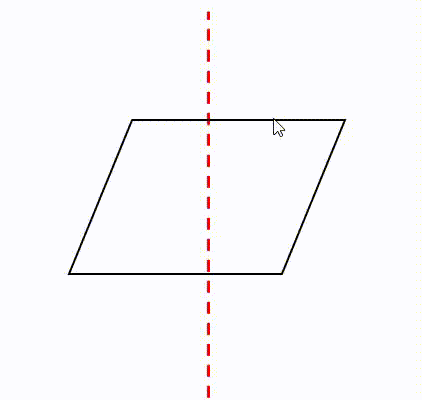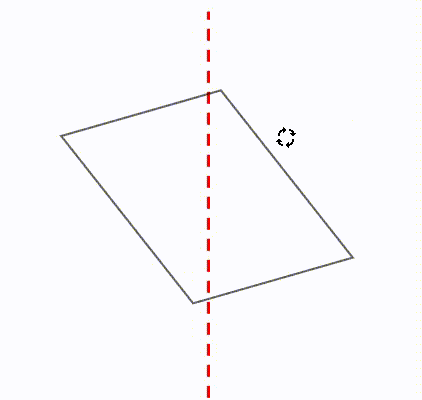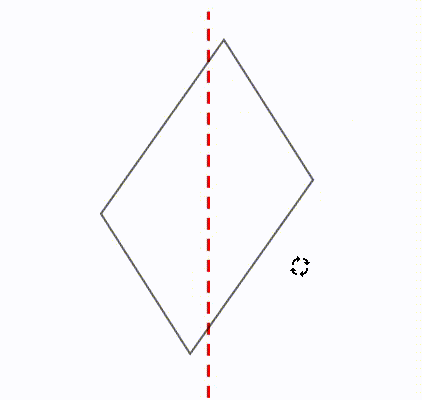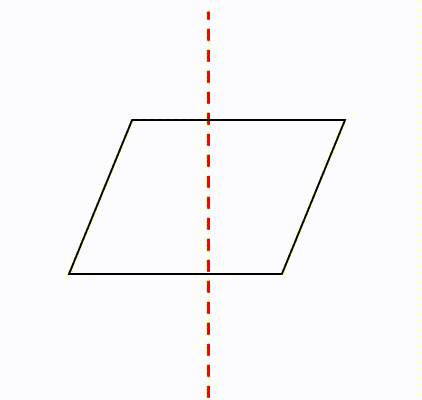



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun




天才ドリル 平面図形が得意になる点描写 点対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon



2




線対称な図形 無料で使える学習ドリル
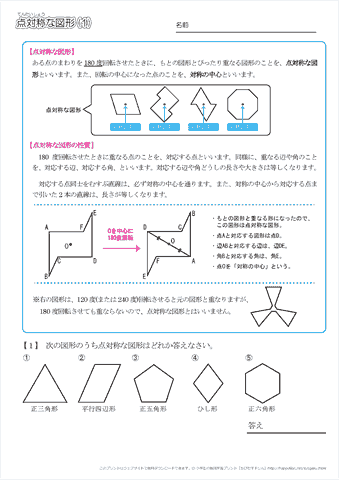



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生




世界一分かりやすい算数 小6 対称な図形
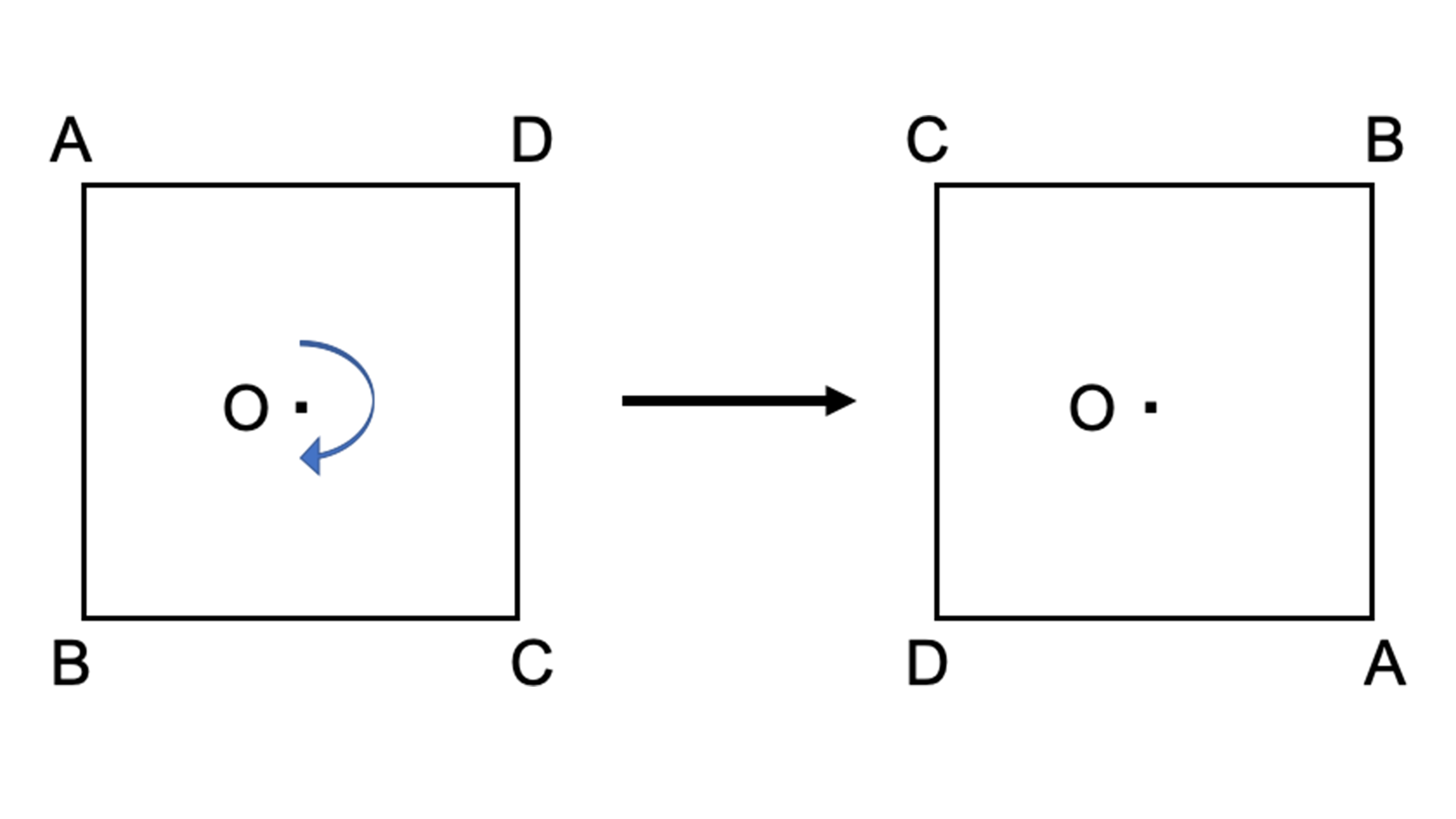



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



中1数学 点対称な図形とは まなビタミン By 東京個別指導学院



対称な図形 たしかめよう 6年生 翁島 おきなしま 小学校ホームページ




線対称 点対称 算数用語集



点対称な図形 問題プリント まとめテスト 小学6年生用無料算数プリント ページ 2



中1数学 点対称な図形とは まなビタミン By 東京個別指導学院



中1数学 点対称な図形とは まなビタミン By 東京個別指導学院



無料 中1数学 基本解説 問題プリント 平面図形2 多角形 点対称 135



6年算数対称な図形2 正多角形教え方
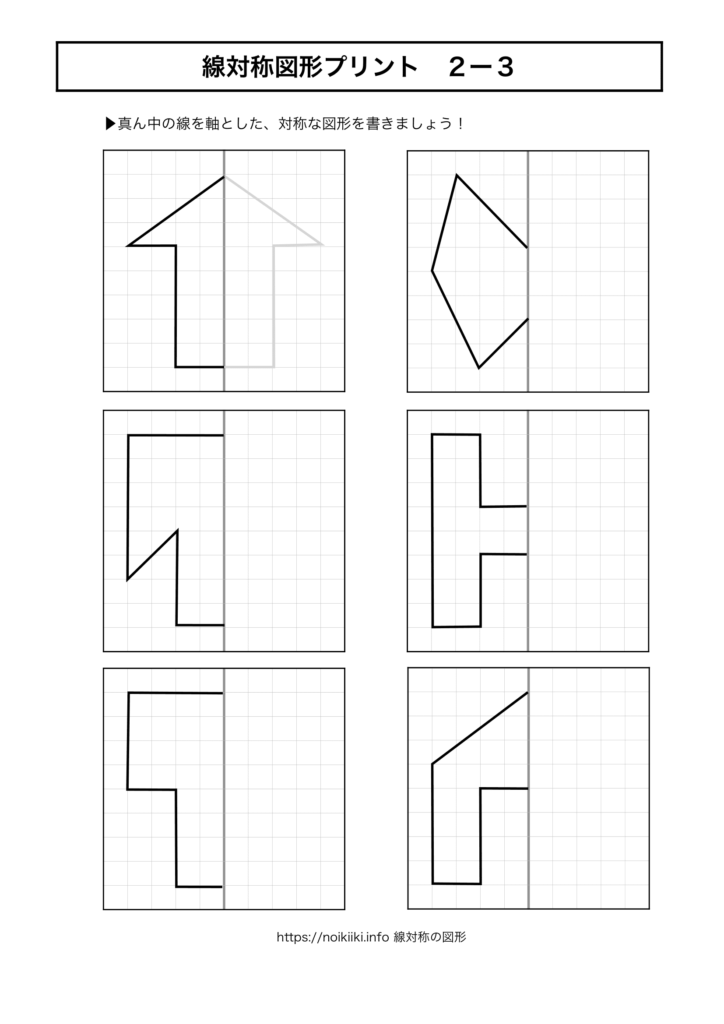



線対称図形プリント2ー3 使える 無料プリント教材 Noikiiki



無料 中1数学 発展問題 問題プリント 平面図形4 円 対称
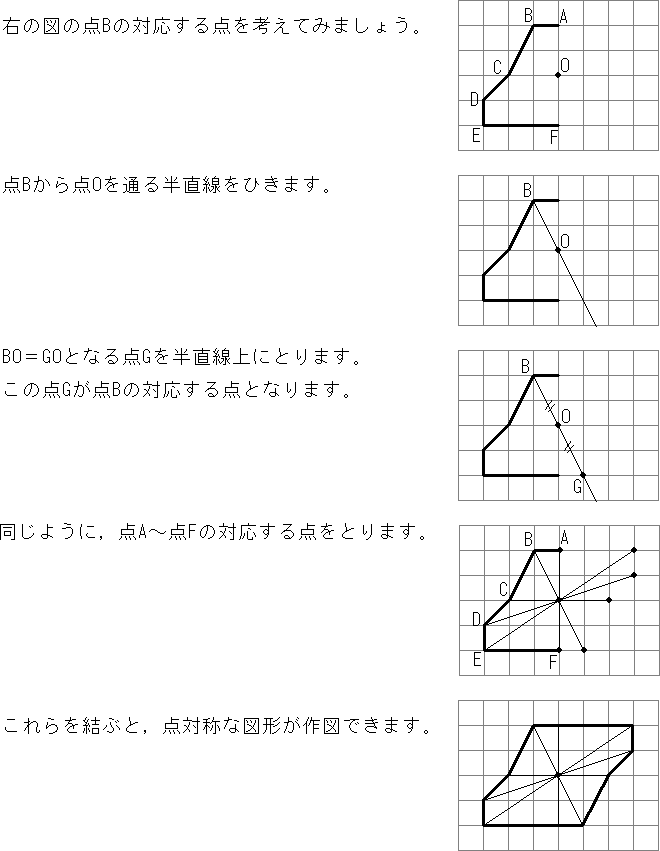



点対称な図形のかき方 中学数学 定期テスト対策 ベネッセ教育情報サイト



2
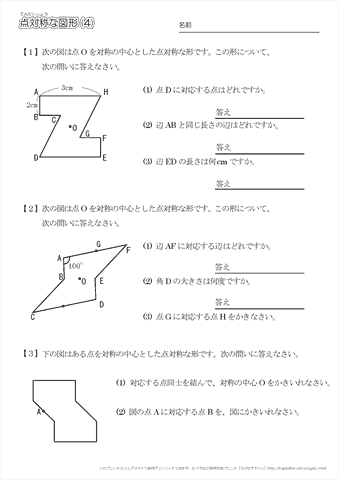



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生




2
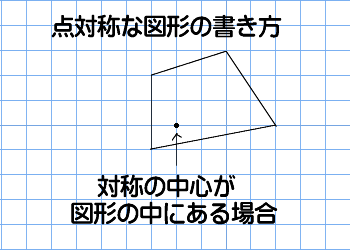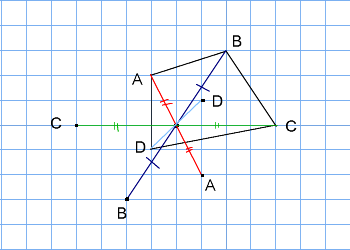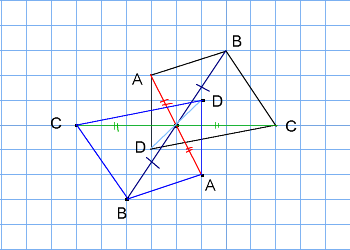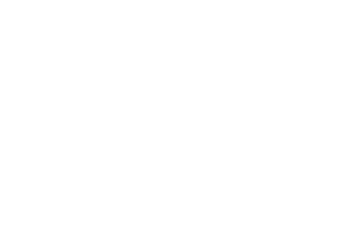



6年算数 対称な図形 わかる教え方
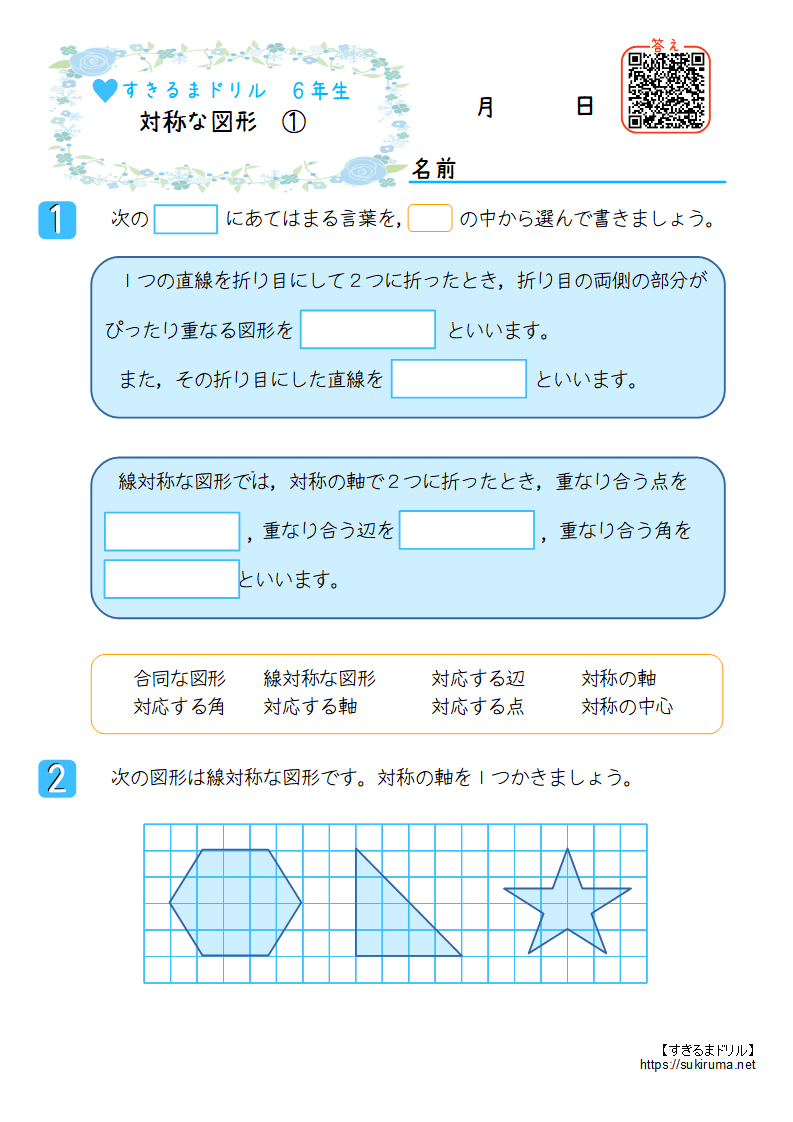



すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント



Q Tbn And9gctrrevlnjrdnbu7lj 4vcerlejy5dvea 9iptz2pitgqmwmpsad0uyh Usqp Cau
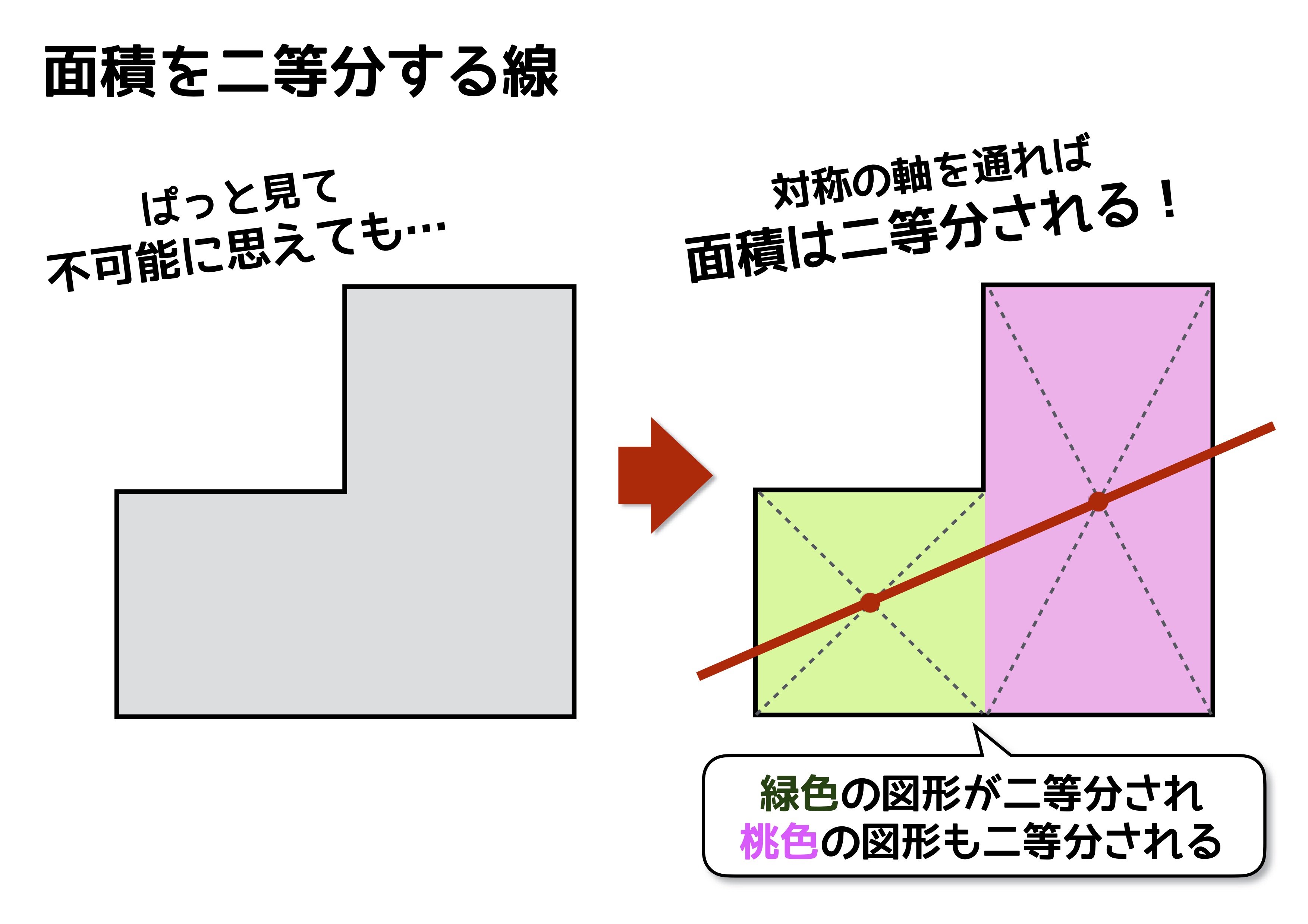



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
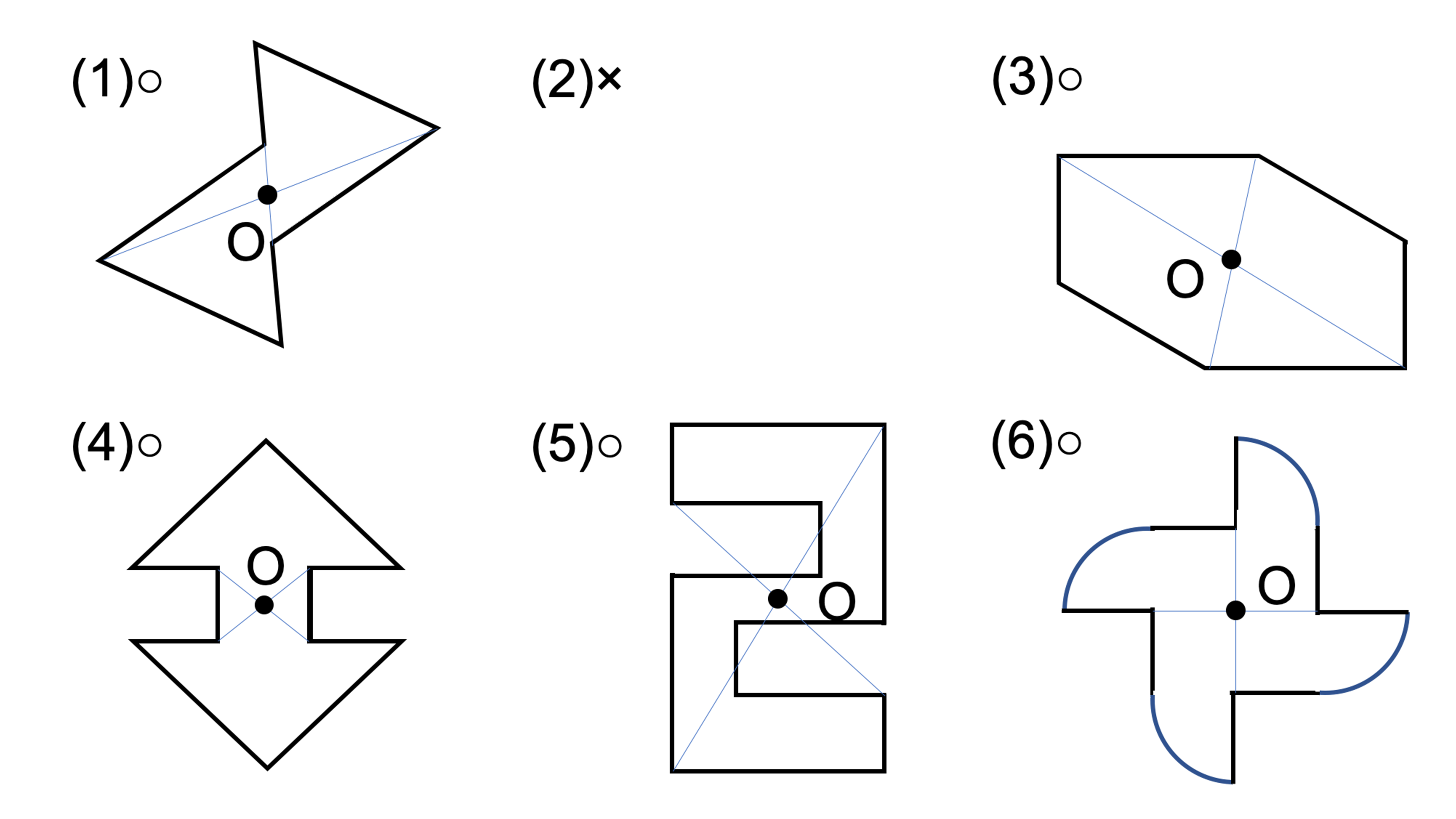



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
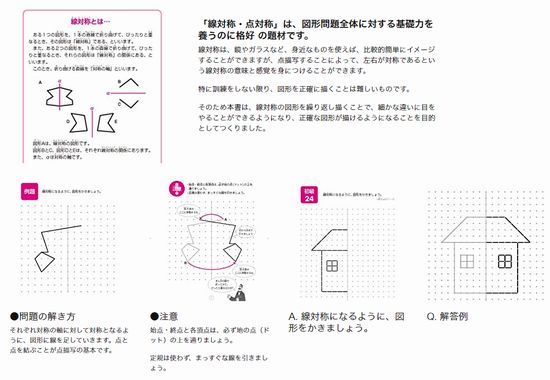



天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 絵本ナビ 認知工学 みんなの声 通販



Math 点対称な図形のかき方 働きアリ The 2nd
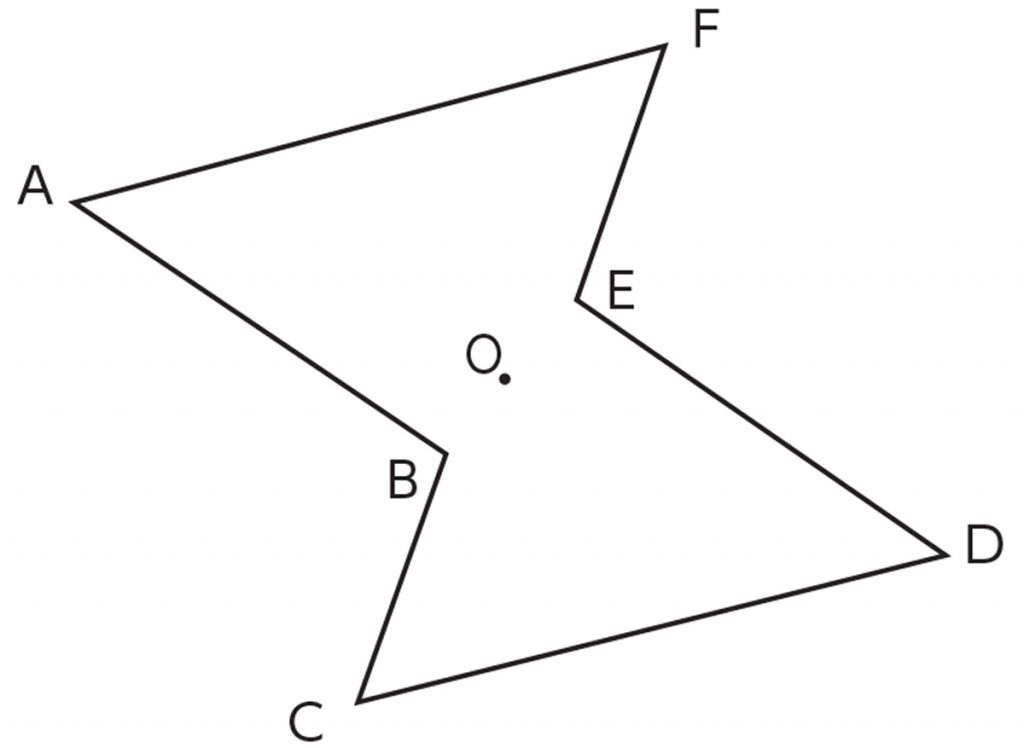



小6算数 点対称な図形の性質 指導アイデア みんなの教育技術
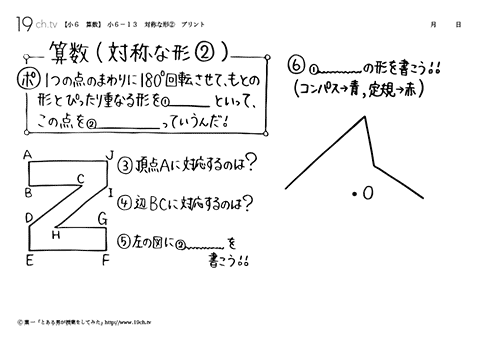



小学6年生の算数 動画 対称な形 の問題 19ch 点対称
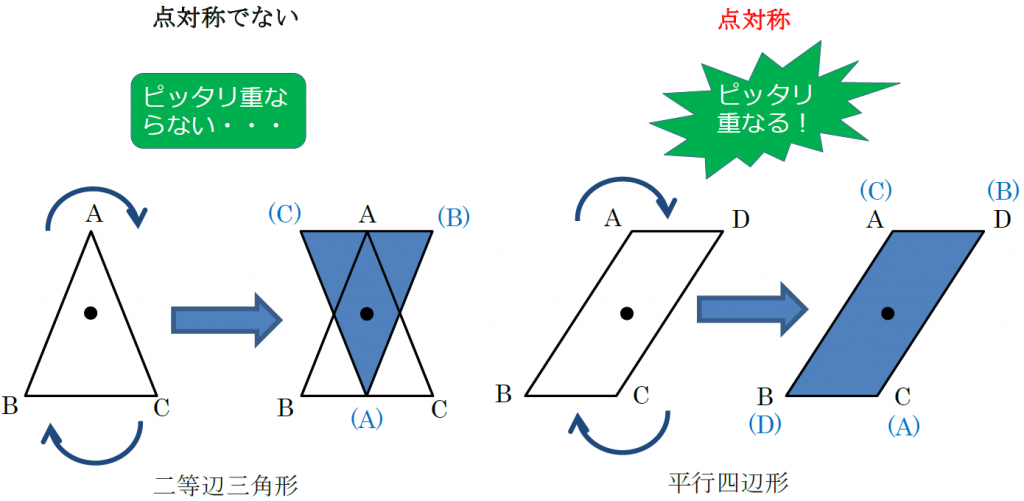



中1数学 点対称な図形とは まなビタミン By 東京個別指導学院



中1数学 平面図形3 点対称 点対称2 発展問題 問題 137 プリント




算数 対称な図形 問題の工夫



Studydoctor線対称 点対称な図形の書き方 中学1年数学 Studydoctor
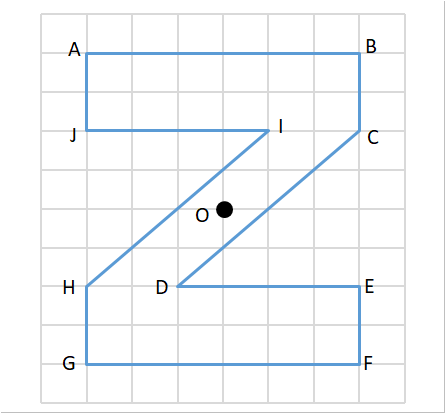



対称な図形 点対称 対称の軸 対応する点 中心を通り同距離




天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon




線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学



無料 中1数学 基本問題 解答プリント 平面図形2 多角形 点対称 135
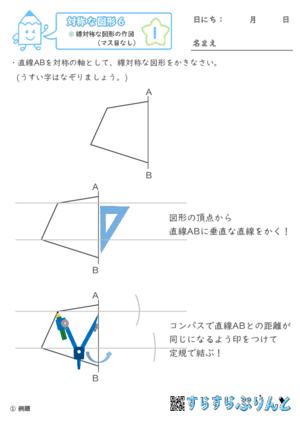



線対称な図形の作図 マス目なし 対称な図形 小6算数




世界一分かりやすい算数 小6 対称な図形
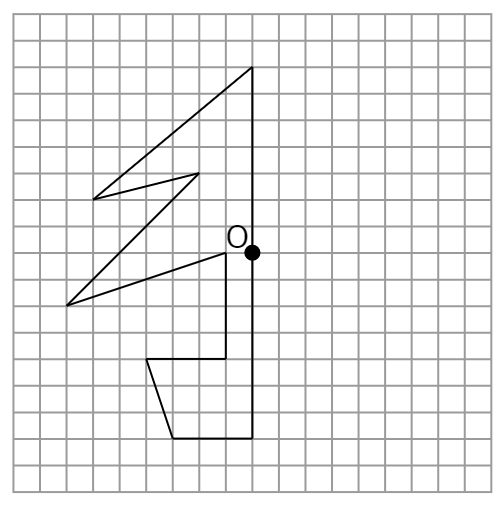



点対称な図形 問題プリント まとめテスト 小学6年生用無料算数プリント



無料 中1数学 基本問題 問題プリント 平面図形2 多角形 点対称 135
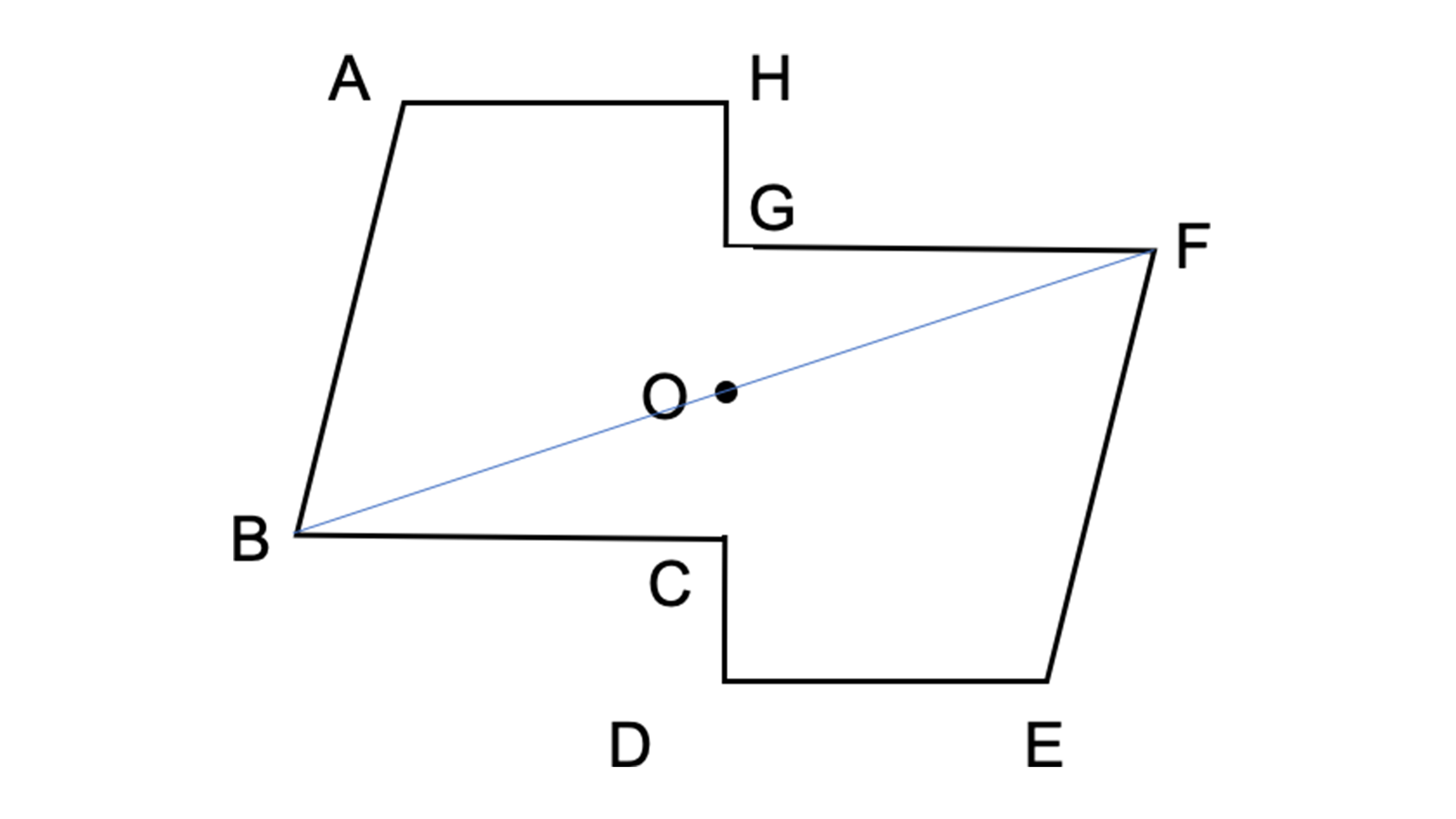



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




線対称な図形 無料で使える学習ドリル




スマホok 6年 対称な図形 難問に挑戦しよう Youtube
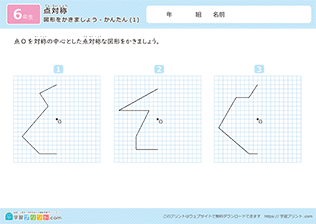



2




線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun




塾 学校 家庭を結ぶ 受験情報サイト 学びネット
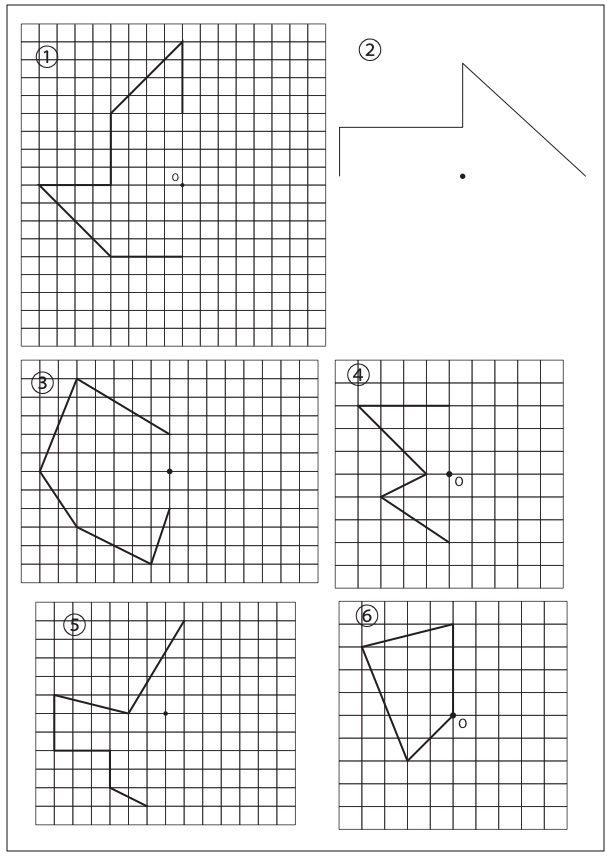



6年算数 対称な図形 点対称 作図練習プリント ネコ好きな学校の先生の日常
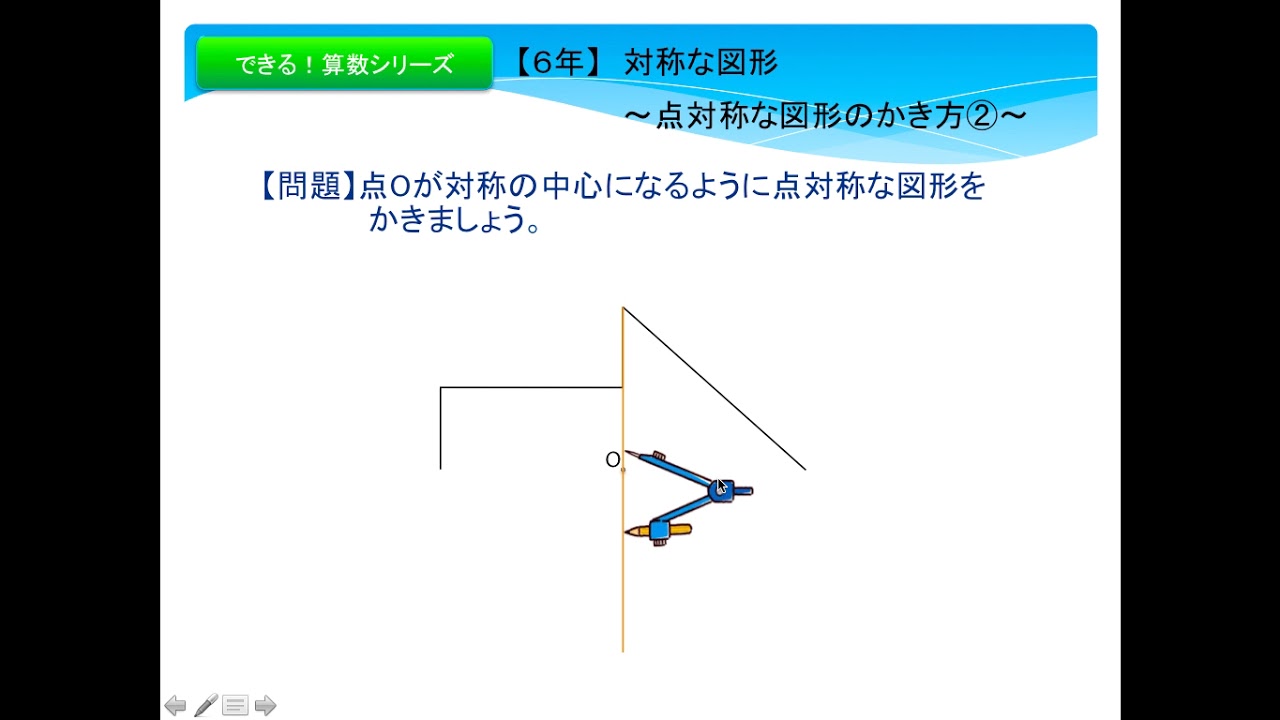



スマホok 6年 対称な図形 点対称な図形のかき方 Youtube
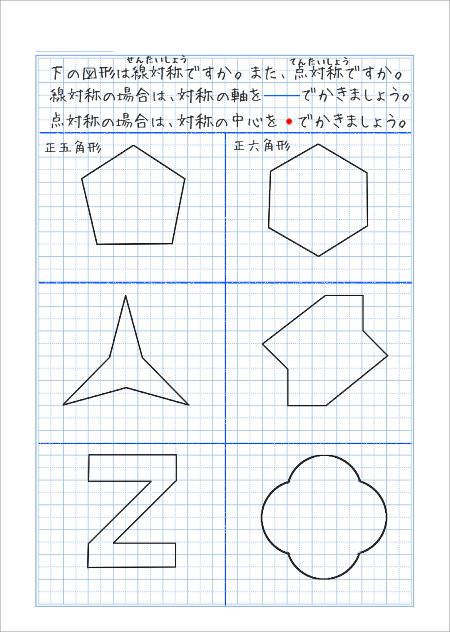



線対称と点対称の自主学習ノート 家庭学習レシピ




対称な図形 Ict教材eboard イーボード




対称な図形 まとめ 無料で使える学習ドリル
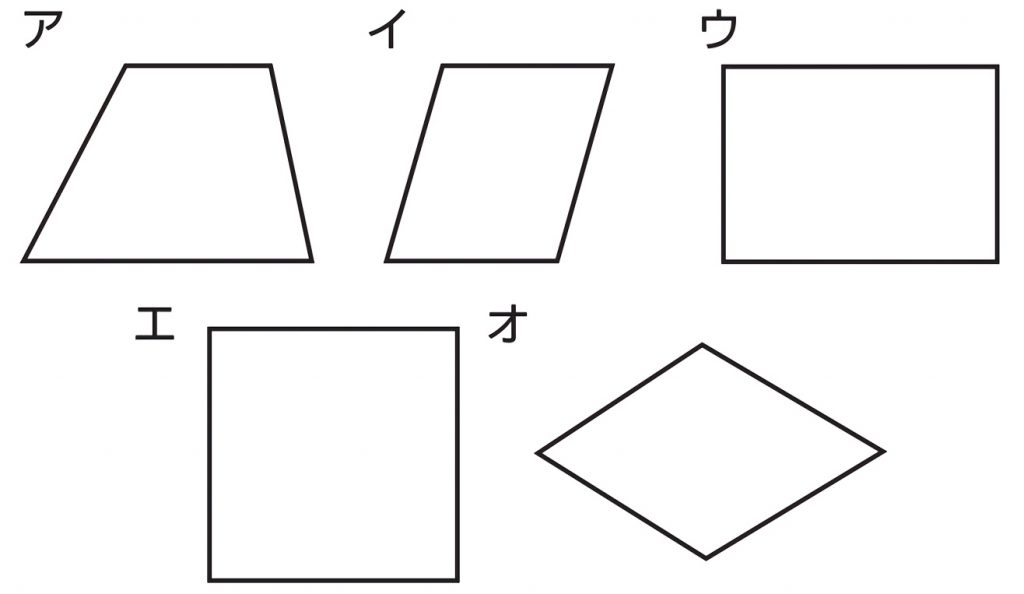



小6算数 多角形と対称 指導アイデア みんなの教育技術




小6算数 対称な図形 学習プリント 練習問題 無料ダウンロード印刷




点対称な図形 無料で使える学習ドリル
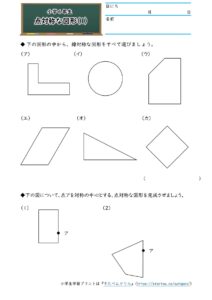



小6算数 対称な図形 学習プリント 練習問題 無料ダウンロード印刷



中学生の数学講座 図形と作図
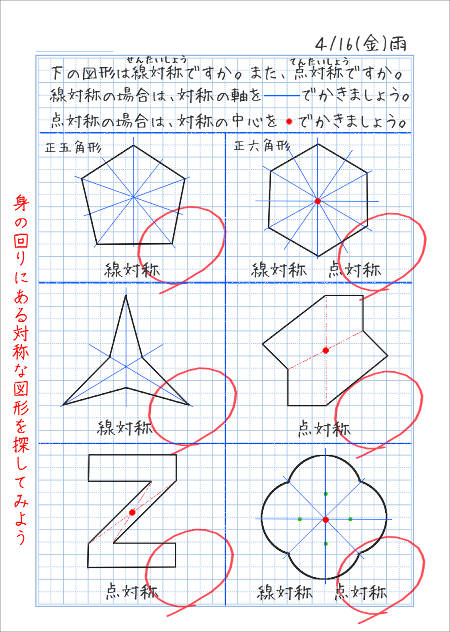



線対称と点対称の自主学習ノート 家庭学習レシピ




スマホok 6年 対称な図形 算数をつかってやってみよう 線対称や点対称な図形をかいてみよう Youtube



対称な図形と回転 桐朋中学 12年 どう解く 中学受験算数




世界一分かりやすい算数 小6 対称な図形




小6で習う 対称な図形 を アートのアプローチで楽しく学べる 点対称アート って Math Channel Magazine




線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学
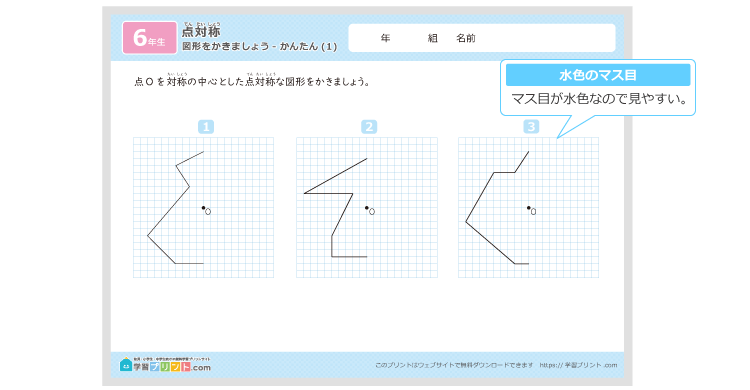



2
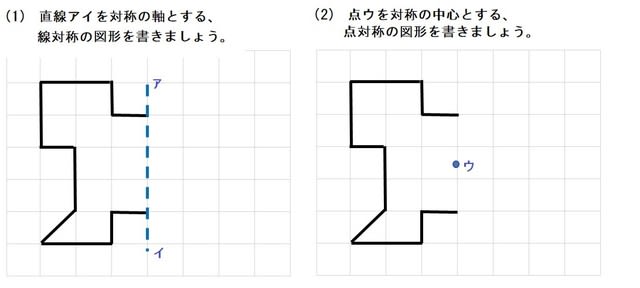



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support




6年生 線対称と点対称 クリヤキン Note
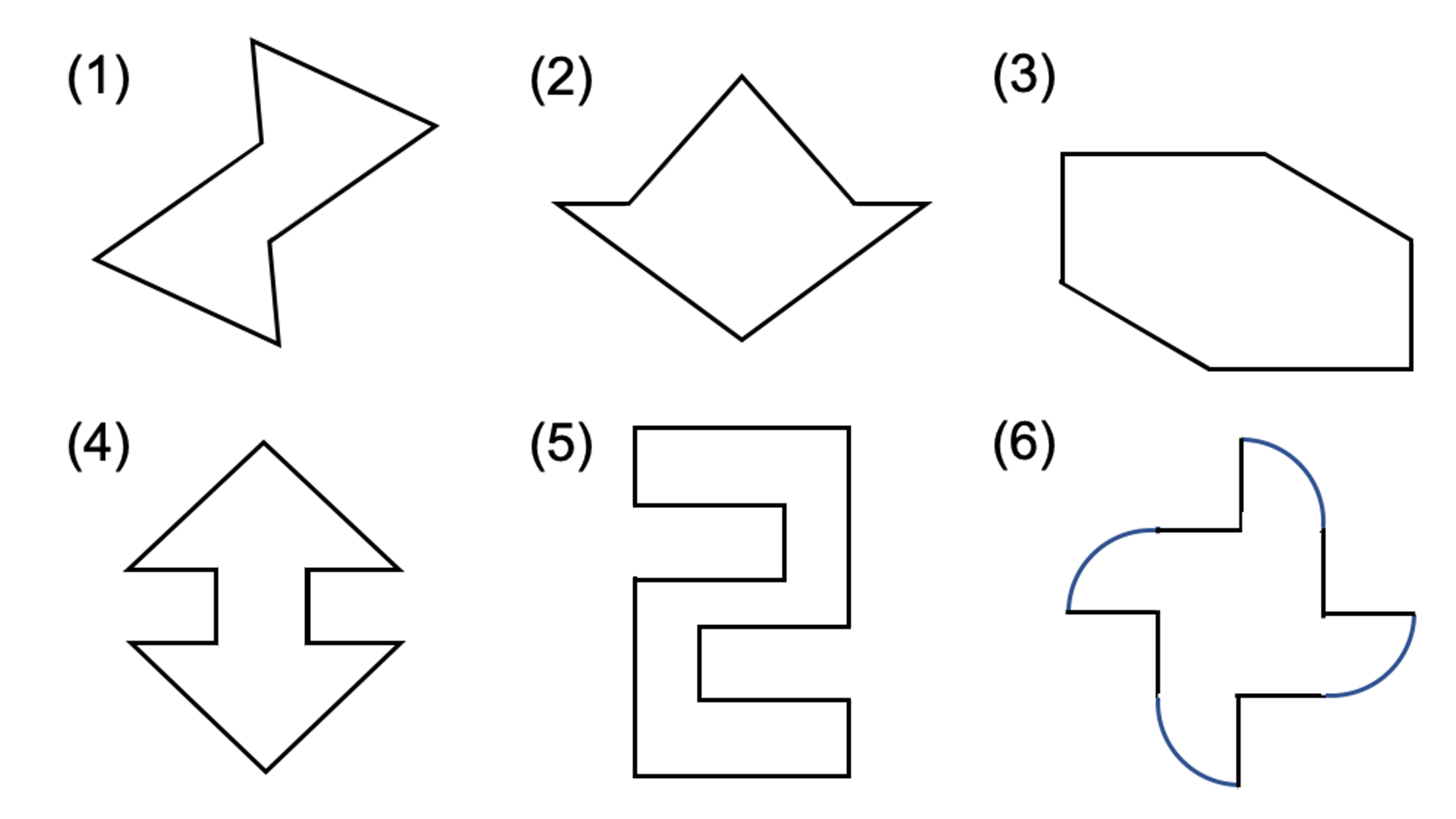



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




点対称な図形 無料で使える学習ドリル
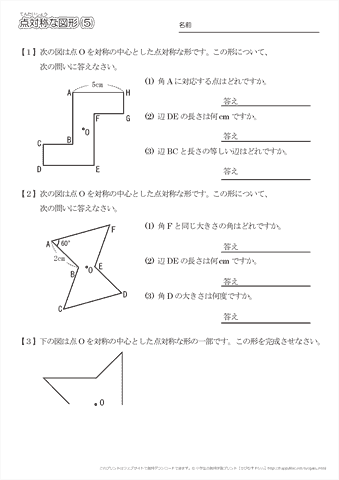



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
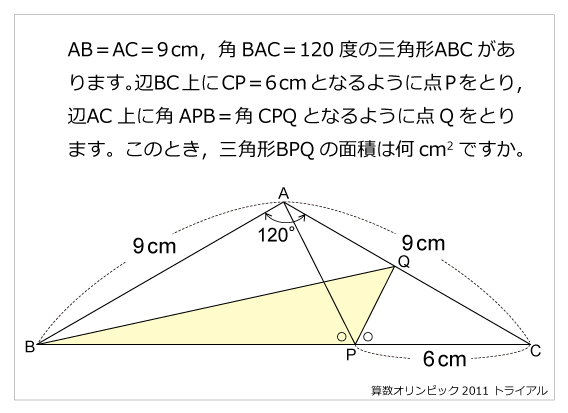



線対称 算数星人のweb問題集 中学受験算数の問題に挑戦



Q Tbn And9gcstg8k8s2os65 Hx5ab1euvmjahwcwee76woxty7p6rhuknr7ndvmdx Usqp Cau



点対称な図形の対応する頂点を確認する Ipadとiphoneで教師の仕事をつくる
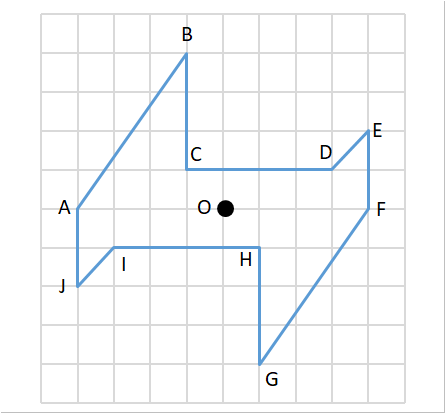



対称な図形 点対称 対称の軸 対応する点 中心を通り同距離
コメント
コメントを投稿